Point: 100
Due Date: Friday February 12th, 5:00pm
See the attached file in PDF.
Create Your RV Bank
Point:![]()
Due Date: Monday February 15th, 2:00pm
- Digital submission
Use Microsoft Excel. Generate 400 random numbers from U (0,1). After fixing them, organize them into 20 rows and 20 columns (only 3 digits after the decimal). You will be using this set in later assignments, So make sure to save a copy for your future use. For future reference, We call this set your RV Bank so when you are asked to use your RV Bank you know where to look for the information. Send a PDF copy of the file to me (remember to use correct naming format). All references to elements of the RV Bank are in matrix format. For example, when you need to to start from (12,4), the reference is to the value at 12th row and 4th column.
Assignment # 2: Probability and Random Number Generation -1
Point:150
Due Date: Friday February 19, 5:00pm
Use Maple software. From the Help menu select New User' Tour. Study the tour pages and then perform the followings:
Use Excel and your RV Bank. For each row, find the average. Use these 20 averages that you have calculated and find their mean., variance , and standard deviation (SD). Use these values in Maple to define a function using the
where
~ Normal
.
Find the integral of the function for (,
), (
,
),
,

, and (0.423, 0.629).
Use the Standard Normal tables from your Probability/Statistics textbook to find the same values and compare them with the results obtained from Maple.
Use Maple to find P (


) where
is exponentially distributed with

and compare that value with direct calculation by analytical methods.
Calculate P (

) where
~ Poisson (
) both analytically and using Maple.
Use the formula provided in random number generation lecture notes to generate 400 random numbers from exponential distribution with the mean of 4.09.
Graph the theoretical
and F (x) functions for Exponential distribution of Part 5 . (If you do not recall the formulas from the probability class, here is a nice gallery of common distribution from Engineering Statistics Handbook at NIST).
Sort your 400 generated numbers in ascending order. Find the range (largest value - smallest value). Divide the range into 10 equal intervals. Count the number of occurrences in each interval. Plot a histogram where the abscissa is represented by integer values from 0 to an integer number larger than the maximum value of the numbers you have obtained and the ordinate is the frequency (count on each interval divided by 400).Visually compare the the obtained histogram to the theoretical
one and draw possible conclusions.
Use the ten frequencies you have found in previous step in the same order they are. Find the cumulative values of the frequencies as follows: first cumulative value is the first frequency value, second cumulative value is sum of the first and second frequencies obtained, third cumulative value is sum of the first, second, and third frequencies obtained and so on. Create a plot that its ordinate represents cumulative frequency values and its abscissa has the same values as the ones in your histogram. Plot the 10 points on this graph with the following coordinates: (upper end of the interval, cumulative frequency). Visually compare the the obtained plot to the theoretical F (x) and draw possible conclusions.
Use Maple to graph the pdf of exponential, normal and Weibull distributions for different values of their parameters and make statements of what happens when the parameters increase or decrease based on the obtained graphs. Do not overdo it, 4 or 5 graph for each parameter is enough. Totally 4 graphs are needed, graph one for exponential parameter
, graph two for Normal parameter
, graph three for Weibull parameter
and graph 4 for Weibull parameter
. Make sure to annotate the graphs.
Use your RV Bank. Starting from the third column for this assignment use the numbers in that column is the same order. If more numbers are needed use the fourth column. In each case, all calculations must be shown, but explanation is not needed on similar steps. For example, for question one below, fully explain how the random number is calculated for the first number that you find, but do not need to explain for the other four numbers, just show the calculations.
- Generate 3 random numbers from Bernoulli (0.373) .
- Generate 3 random numbers from U (1.09, 3.94) .
- Generate 3 random numbers from EXP (5.95) .
- Generate 2 random numbers from Poisson (5.86) .
- Generate 4 random numbers from N (2.49, 0.36) .
Assignment # 3: Random Number Generation-2
Point: 90
Due Date: Thursday February 25th, 2:00pm
Use your RV Bank. Starting from (5,5) for this assignment use the numbers row-wise. In each case, all calculations must be shown, but explanation is not needed on similar steps. For example, for question one below, fully explain how the random number is calculated for the first number that you find, but do not need to explain for the other four numbers, just show the calculations.
- Generate 5 random numbers from Geom (0.398) .
- Generate 5 random numbers from Bin (4, 0.398) .
- Generate 5 random numbers from Negbin (3, 0.398) .
- Generate 5 random numbers from Triang (4,8,11) .
- Generate 2 random numbers from Gamma (0.792, 4.39)
- Generate 2 random numbers from Gamma (4.39, 0.77) .
- Generate all possible random numbers by the LCG with m=39, a=3, c=15 and X0 =22. What is
5831 for this LCG?
Assignment # 4: Random Number Generation - 3
Point: 80
Due Date: Monday February 29th, 5:00pm
Use your RV Bank for this assignment. Start with random number at (13,8) and continue using numbers in rows. Please note that this assignment is not on Excel or Maple. All calculations must be shown in your report. however, make sure to use Excel to verify your calculations.
- In an international archery competition four finalists are competing against each other. Each archer will have four tries to hit a target 100 yards away. Archers will receive points based on how close to the center of target their arrows hit.10 points for area with the diameter of 1 inch from the center, 7 points for area between 1 and 3 inches from the center, 3 points for area between 3 and 5 inches from the center, and 1 point for area between 5 and 10 inches from the center are awarded. If an arrow hit outside the 10 inch diameter area, the archer would lose 2 points. Based on the past performance records of the archers, the probabilities of hitting the three high point targeting areas for each archer, at any condition, is given as (0.23, 0.29, 0.31), (0.19, 0.23, 0.37), (0.16, 0.38, 0.30), and (0.15, 0.33, 0.44) respectively. All finalists have the same low probability of missing the target board of 5 percent. Each archer finishes all his shots before the next archer begins. Simulate the competition (one run) and identify the winner. Also answer the following two what-if type scenarios: What if you used the same numbers you generated before but changed the arrangement of the competition so all archers will do one shot per round? Would the winner be different? Answer without performing the simulation. Back up your claim with sound explanation. What if competitors are blind-folded, hanging from trees with Bungee Jumping string tied to one leg with a 100-pound baby African gorilla hanging to other leg, only 4 feet above a pond with hungry crocodiles and a volcano about to erupt. Would it make any difference? Why or why not?
- All three-letter English words that begin with a consonant are placed in a bag and one is randomly chosen from the bag, read and placed back in the bag. If the drawn word ends with a vowel reward yourself with an apple. If the drawn word has no other consonants in it, reward yourself with two apples. If none of the above, but the drawn word begins or ends with legitimate letters from the word ENGINEER, reward yourself 3 apples. How many apples do you have after performing the experiment 5 times?
- Generate 5 random numbers from a probability distribution defined below.
















Assignment # 5: Exam 1 Questions
Point: 100
Due Date: Monday March 14th, 3:00pm
Solve and submit problems of Exam 1.
Assignment # 6: SIMIO Modeling 1
Point: 500
Due Date: Tuesday April 5th, 5:00pm
Check Mr. Ashkan Negahban's page at Auburn University and click on Simulation Video Lab Series. There are 8 labs each with introductory videos and an assignment. Watch the videos and submit the assignments.
Assignment # 7: SIMIO Modeling 2
Point: 100
Due Date: Tuesday April 12th, 5:00pm
Solve and submit
Assignment # 8: SIMIO Modeling 3
Point: 100
Due Date: Tuesday April 19th, 5:00pm
Solve and submit
Assignment # 9: Exam 2 Questions
Point: 100 + 20 for Bonus Question
Due Date: Friday April 22nd, 5:00pm
Solve and submit ALL problems of the Exam 2. Note that the SIMIO model need to be actually done with SIMIO.
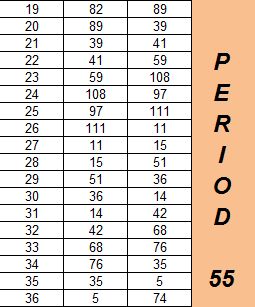
Bonus Question: If you have a partial set of information about a LCG, can you figure out a, c, X0 and m? Show the work by using the following example:
Assignment # 10: SIMIO Modeling 4
Point: 100
Due Date: Tuesday April 26th, 5:00pm
Solve and submit
Assignment # 11: SIMIO Modeling 5
Point: 100
Due Date: Friday April 29th, 5:00pm
Solve and submit
Assignment # 12: SIMIO Modeling 6
Point: 100
Due Date: Friday May 5th, 5:00pm
Solve and submit
Assignment archive from previous classes