Swann's Method
Idea: To find a starting interval for
search methods. Start at some arbitrary initial
trial point (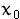 )
and a step-size parameter ( )
and a step-size parameter ( ).
Generate successive points through a recursive relationship and compare the function values at these
successive points. When there is a change in the direction of decrease (for Min problems) the
interval is found. Depending on whether ( ).
Generate successive points through a recursive relationship and compare the function values at these
successive points. When there is a change in the direction of decrease (for Min problems) the
interval is found. Depending on whether (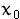 ) is at the right of the actual min or to the right of it, the value of
( ) is at the right of the actual min or to the right of it, the value of
( )
may be positive or negative. the recursive relation is: )
may be positive or negative. the recursive relation is:
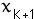

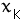

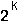
 for
for 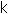 = 0, 1, 2, ... = 0, 1, 2, ...
To identify the sign
 , compare , compare
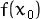 , ,
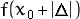 , and , and
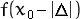 . If: . If:
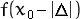
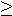
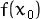
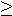
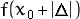 , then sign of , then sign of
 is positive.
If: is positive.
If:
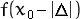
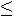
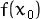
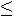
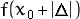 , then sign of , then sign of
 is negative. is negative.
Example:
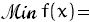 0.1
0.1
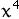 + 0.5 + 0.5
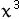 - 3.3 - 3.3
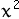 + 11.3 + 11.3
 + 49 + 49
Start by choosing starting point
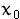
 6.5 and step size
6.5 and step size

 0.5.
Now let's compare
0.5.
Now let's compare
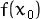 |
= 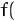 6.5 6.5
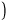 |
= 219.80 |
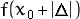 |
=
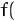 7 7
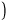 |
= 151.94 |
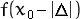 |
=
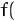 6 6
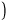 |
= 100.00 |
which indicates the actual minimum is to the left of
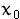 , so , so
 = -
0.5. Now let's generate successive = -
0.5. Now let's generate successive
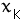 values and compare their
associated f values. values and compare their
associated f values.
Therefore, the search bracket is [-1 , 5 ].
[ Swann's Method ]
[ Interval Halving Method ]
[ Golden Section Method ]
[ Fibonacci Method ]
Interval Halving Method (3-Point Equal Interval Search)
Idea: To find the
minimum of a function by successively reducing the search area in half such that
the final bracket is within the epsilon distance of the actual minimum.
Algorithm: To find the
minimum of
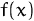 over the search are
( over the search are
( , ,
 ): ):
| Step 1: |
Let
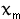 =
( =
(

 )/2 and L = )/2 and L =


 . Compute . Compute
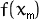 . . |
| Step 2: |
Set
 = =

 L/4 and L/4 and
 = =

 L/4. Compute L/4. Compute
 and
and
 . . |
| Step 3: |
Compare
 and and
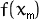
- If

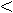
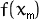 ,
drop interval ( ,
drop interval ( , ,
 ). Set ). Set

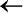
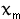 , ,
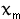
 , ,
 = =
 and
go to Step 5. and
go to Step 5.
- If

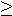
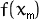 go to
Step 4. go to
Step 4.
|
| Step 4: |
Compare
 and and
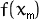
- If

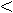
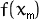 , drop
interval ( , drop
interval ( ,
,
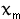 ).
Set ).
Set 
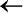
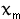 , ,
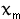
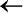
 , ,
 = =
 and go to Step 5. and go to Step 5.
- If

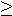
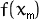 ,
drop both intervals ( ,
drop both intervals ( , ,
 )
and ( )
and ( , ,
 ).
Set ).
Set 
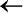
 , ,
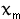 = =
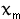 , ,

 and go to
Step 5. and go to
Step 5.
|
| Step 5: |
Compute L =


 . If | L | . If | L |
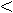
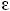 stop.
Otherwise, go to Step 2. stop.
Otherwise, go to Step 2. |
Example:
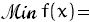 0.1
0.1
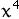 + 0.5 + 0.5
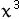 - 3.3 - 3.3
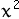 + 11.3 + 11.3
 + 49, + 49,

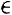 [-1,5],
[-1,5],
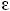 =0.001 =0.001
| Step 1: |
Let
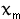 = (-1+5)/2=2 and L =5-(-1)=6. = (-1+5)/2=2 and L =5-(-1)=6.
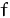 (2)=18.80 (2)=18.80 |
| Step 2: |
Set
 =
-1+6/4=0.5 and =
-1+6/4=0.5 and
 =
5-6/4=3.5. =
5-6/4=3.5.
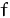 (0.5)=42.59
and (0.5)=42.59
and
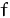 (3.5) =
4.46 (3.5) =
4.46 |
| Step 3: |
 = 42.59
= 42.59

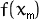 = 18.80. Go
to
Step 4
= 18.80. Go
to
Step 4 |
| Step 4: |
 = 4.46
= 4.46
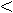
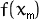 = 18.80. Drop
interval (
= 18.80. Drop
interval ( ,
,
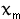 )
= (-1,2).
Set )
= (-1,2).
Set  = 2, = 2,
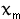 =
3.5, =
3.5,
 = 5 and go to
Step5. = 5 and go to
Step5.
|
| Step 5: |
L = 5 -2 = 3
 0.002, go to Step 2.
0.002, go to Step 2. |
| Step 2: |
Set
 = 2+3/4=2.75 and
= 2+3/4=2.75 and
 =
5-3/4=4.25. =
5-3/4=4.25.
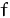 (2.75)=9.086
and (2.75)=9.086
and
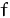 (4.25) =
12.377 (4.25) =
12.377 |
| Step 3: |
 = 9.086
= 9.086

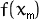 = 4.46. Go to Step 4
= 4.46. Go to Step 4 |
| Step 4: |
 = 12.377
= 12.377

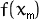 = 4.46. drop both intervals (
= 4.46. drop both intervals ( , ,
 )
= (2,2.75) and ( )
= (2,2.75) and ( , ,
 )
= (4.25,5). )
= (4.25,5).
 =2.75, =2.75,
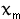 =3.5, =3.5,
 =4.25, Go to
Step 5. =4.25, Go to
Step 5. |
| Step 5: |
L = 4.25 - 2.75 = 1.5
 0.002, go to Step 2.
0.002, go to Step 2. |
| Step 2: |
Set  = 2.75+1.5/4=3.125 and
= 2.75+1.5/4=3.125 and  = 4.25-1.5/4=3.875. = 4.25-1.5/4=3.875.
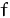 (3.125)=6.256 and (3.125)=6.256 and
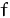 (3.875) = 7.300 (3.875) = 7.300 |
| Step 3: |
 = 6.256
= 6.256

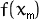 = 4.46. Go to Step 4
= 4.46. Go to Step 4 |
| Step 4: |
 = 7.300
= 7.300

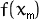 = 4.46. drop both intervals (
= 4.46. drop both intervals ( , ,
 )
= (2.75, 3.125) and ( )
= (2.75, 3.125) and ( , ,
 )
= (3.875, 4.25). )
= (3.875, 4.25).
 = 3.125, = 3.125,
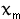 =3.5, =3.5,
 = 3.875. Go to
Step 5. = 3.875. Go to
Step 5. |
| Step 5: |
L = 3.875 - 3.125 = 0.75
 0.002, go to Step 2.
0.002, go to Step 2. |
In three iterations the interval of search has been reduced to one-eighth of the initial
search interval. In general after n iterations there the search interval will be reduced to
( -
- ) )
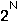 . So, to get to
the required . So, to get to
the required 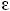 value (0.001) we need to solve 6
value (0.001) we need to solve 6 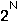
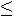 0.001 from which
N 0.001 from which
N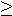 13 or 10 more
iterations. For further discussion on termination rules, please see the discussion at
the bottom of this page.
[ Swann's Method ]
[ Interval Halving Method ]
[ Golden Section Method ]
[ Fibonacci Method ] 13 or 10 more
iterations. For further discussion on termination rules, please see the discussion at
the bottom of this page.
[ Swann's Method ]
[ Interval Halving Method ]
[ Golden Section Method ]
[ Fibonacci Method ]
Golden Section Method
Idea: Interval Halving method requires two
function evaluations at each iteration. Golden Section method uses only one
function evaluation at every iteration (after the first iteration). Two
points
 and and
 are placed are placed
 units from each end
of the search interval of one
unit length. For length L, the placements would be units from each end
of the search interval of one
unit length. For length L, the placements would be
 L from each end.
Alternatively, a change of variable from L from each end.
Alternatively, a change of variable from
 to to
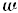 such that
such that 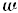  (
(

 ) )
 (
(

 ) or ) or

 (
(


 ) )
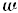

 and minimizing and minimizing
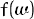 instead of instead of
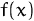 will result in the search interval of 1 unit. So, the first placement of points
will result in the search interval of 1 unit. So, the first placement of points
 and and
 will be at points (
will be at points (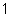 

 0.382)
and (
0.382)
and ( =0.618)
from left. Now compare =0.618)
from left. Now compare
 and
and  and based on
that comparison discard the smaller portion of the search interval such that the and based on
that comparison discard the smaller portion of the search interval such that the
 with the smaller with the smaller
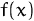 remains in
the larger remaining portion. Now the search interval is reduced to remains in
the larger remaining portion. Now the search interval is reduced to
 with one point in it with the golden ration. Find the position of the
other point
with one point in it with the golden ration. Find the position of the
other point  L
1 L
1

 . .


 2 units from the appropriate end of the line.
Note that in this stage we only generate one new point
2 units from the appropriate end of the line.
Note that in this stage we only generate one new point
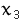 and compare its
value with the and compare its
value with the
 or or
 remaining from
previous stage. After comparison and
elimination of the smaller piece, the new interval of search will be equal to remaining from
previous stage. After comparison and
elimination of the smaller piece, the new interval of search will be equal to
 2
.Generally, at the end of Nth iteration, the interval of search is L
N 2
.Generally, at the end of Nth iteration, the interval of search is L
N

 N
(L 0). The number of function evaluations is N
N
(L 0). The number of function evaluations is N 1
(initially we need two points to start with). We also need to to perform a
test similar to Step 5 of the Interval Halving algorithm for termination
purposes. Here is an algorithm for the implementation of Golden Section Method. 1
(initially we need two points to start with). We also need to to perform a
test similar to Step 5 of the Interval Halving algorithm for termination
purposes. Here is an algorithm for the implementation of Golden Section Method.
Algorithm: To find the
minimum of
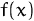 over the search are
( over the search are
( , ,
 ): ):
| Step 1: |
Let

 0.618,
1
0.618,
1

 0.382,
0.382,

 (
(

 )
(1 )
(1
 ) )

 , ,
 =
( =
(

 )
( )
( ) )

 . Compute . Compute
 , ,
 |
| Step 2: |
Compare
 and and

- If

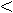
 ,
drop interval ( ,
drop interval ( , ,
 ]. Set: ]. Set:





 =( =(

 )
(1 )
(1
 ) )


and go to
Step 3.
- If


 ,
drop interval [ ,
drop interval [ , ,
 ). Set: ). Set:




 =
( =
(

 )
( )
( ) )


and go to
Step 3.
|
| Step 3: |
If |


 . | . |
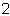
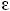 stop.
Otherwise, compute stop.
Otherwise, compute
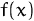 for the new point and go to Step 2.
for the new point and go to Step 2. |
Example: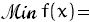 (
(

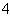 )
2 )
2

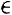 [2 ,5],
[2 ,5],
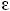 =0.001 =0.001
| Step 1: |
 = 2,
= 2,  = 5,
= 5,  = 0.618,
1 = 0.618,
1
 = 0.382, = 0.382,
 = (5 = (5
 2)(0.382)
2)(0.382) 2
= 3.146, 2
= 3.146,
 =(5 =(5
 2)(0.618)
2)(0.618) 2
= 3.854, 2
= 3.854,
 = 0.7293,
= 0.7293,
 = 0.0213
= 0.0213 |
| Step 2: |
 =0.7293 =0.7293
 0.0213=
0.0213= ,
drop interval [2, 3.146). Set: ,
drop interval [2, 3.146). Set:
 =3.1460 =3.1460
 =3.8540 =3.8540
 =0.0213 =0.0213
 = (5 = (5
 3.1460)(0.618) 3.1460)(0.618) 3.1460=4.2917 3.1460=4.2917
and
go to Step 3.
|
| Step 3: |
| 5-3.1460 |
 0.002,
0.002,
 =0.0850
and go to Step 2. =0.0850
and go to Step 2. |
| Step 2: |
 =0.0213 =0.0213
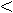 0.0850=
0.0850= ,
drop interval (4.2917, 5]. Set: ,
drop interval (4.2917, 5]. Set:
 =4.2917 =4.2917
 =3.8540 =3.8540
 =0.0213 =0.0213
 =(4.2917-3.1460)(0.382) =(4.2917-3.1460)(0.382) 3.1460=3.5836 3.1460=3.5836
and
go to Step 3. |
| Step 3: |
| 4.2917-3.1460 |
 0.002,
0.002,
 =0.1733
and go to Step 2. =0.1733
and go to Step 2. |
| Step 2: |
 =0.1733 =0.1733
 0.0213=
0.0213= ,
drop interval [3.146, 3.5836). Set: ,
drop interval [3.146, 3.5836). Set:
 =3.5836 =3.5836
 =3.8540 =3.8540
 =0.0850 =0.0850
 = (4.2917
= (4.2917
 3.5836)(0.618) 3.5836)(0.618) 3.5836=4.0212 3.5836=4.0212
and
go to Step 3. |
| Step 3: |
| 4.2917-3.5836 |
 0.002,
0.002,
 =0.0004
and go to Step 2. =0.0004
and go to Step 2. |
| Step 2: |
 =0.0850 =0.0850
 0.0004=
0.0004= ,
drop interval [3.5836, 3.8540). Set: ,
drop interval [3.5836, 3.8540). Set:
 =3.8540 =3.8540
 =4.0212 =4.0212
 =0.0004 =0.0004
 = (4.2917
= (4.2917
 3.8540)(0.618) 3.8540)(0.618) 3.8540=4.1245 3.8540=4.1245
and
go to Step 3. |
| Step 3: |
| 4.2917-3.8540 |
 0.002,
0.002,
 =0.0155
and go to Step 2. =0.0155
and go to Step 2. |
| Step 2: |
 =0.0004 =0.0004
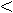 0.0155=
0.0155= ,
drop interval (4.1245,4.2917]. Set: ,
drop interval (4.1245,4.2917]. Set:
 =4.1245 =4.1245
 =4.0212 =4.0212
 =0.0004 =0.0004
 =(4.1245-3.8540)(0.382) =(4.1245-3.8540)(0.382) 3.8540=3.9573 3.8540=3.9573
and
go to Step 3. |
| Step 3: |
| 4.1245-3.8540 |
 0.002,
0.002,
 =0.0018
and go to Step 2. =0.0018
and go to Step 2. |
| Step 2: |
 =0.0018 =0.0018
 0.0004=
0.0004= ,
drop interval [3.854, 3.9573). Set: ,
drop interval [3.854, 3.9573). Set:
 =3.9573 =3.9573
 =4.0212 =4.0212
 =0.0004 =0.0004
 = (4.1245
= (4.1245
 3.9573)(0.618) 3.9573)(0.618) 3.9573=4.0606 3.9573=4.0606
and
go to Step 3. |
| Step 3: |
| 4.1245-3.9573 |
 0.002,
0.002,
 =0.0036
and go to Step 2. =0.0036
and go to Step 2. |
| Step 2: |
 =0.0004 =0.0004
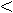 0.0036=
0.0036= ,
drop interval (4.0606,4.1245]. Set: ,
drop interval (4.0606,4.1245]. Set:
 =4.0606 =4.0606
 =4.0212 =4.0212
 =0.0004 =0.0004
 =(4.0606-3.9573)(0.382) =(4.0606-3.9573)(0.382) 3.9573=3.9967 3.9573=3.9967
and
go to Step 3. |
| Step 3: |
| 4.0606-3.9573 |
 0.002,
0.002,
 =0.00001
and go to Step 2. =0.00001
and go to Step 2. |
In eight iterations the interval of search has been reduced to 0.1033 or
less than 3.5% of the original interval of search [2,5]. If you made a
similar comparison for the function values the difference is less than 0.0004.
For further discussion on termination rules, please see the discussion at
the bottom of this page.
[ Swann's Method ]
[ Interval Halving Method ]
[ Golden Section Method ]
[ Fibonacci Method ]
Fibonacci Method
Idea: This search method is similar to the
Golden Section method except that instead of using the golden ration ( )
we use numbers generated from the Fibonacci sequence. Every Fibonacci
number is generated by adding two immediately preceding numbers in the sequence
with the first two initial numbers being 1 and 1. So, F0=1, F1=1,
and Fk = Fk-2 +Fk-1 for k>=2. For
example, the first 11 Fibonacci numbers are F0=1, F1=1, F2=2,
F3=3, F4=5, F5=8, F6=13, F7=21,
F8=34, F9=55, F10=89 and F11=144.
Fibonacci search requires that the number of functional evaluations be specified
in advance such that the position of the first two evaluations can be determined.
Assuming that )
we use numbers generated from the Fibonacci sequence. Every Fibonacci
number is generated by adding two immediately preceding numbers in the sequence
with the first two initial numbers being 1 and 1. So, F0=1, F1=1,
and Fk = Fk-2 +Fk-1 for k>=2. For
example, the first 11 Fibonacci numbers are F0=1, F1=1, F2=2,
F3=3, F4=5, F5=8, F6=13, F7=21,
F8=34, F9=55, F10=89 and F11=144.
Fibonacci search requires that the number of functional evaluations be specified
in advance such that the position of the first two evaluations can be determined.
Assuming that 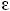 is given, we find the k that satisfies 1
is given, we find the k that satisfies 1 Fk Fk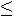 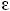 .
For example, if .
For example, if 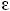 =0.01,
then 1 =0.01,
then 1 Fk Fk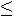 0.01
or Fk 0.01
or Fk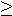 100 suggesting that k=11 in the from the Fibonacci series. Therefore, eleven
evaluations are needed. A similar algorithm to that of Golden Section can
be used except that placement of the points uses the ratio of Fk-1
100 suggesting that k=11 in the from the Fibonacci series. Therefore, eleven
evaluations are needed. A similar algorithm to that of Golden Section can
be used except that placement of the points uses the ratio of Fk-1 Fk
instead of Fk
instead of  . Contrary
to golden ration, . Contrary
to golden ration,  which is fixed, this ratio changes at every iteration
starting from Fk-1 which is fixed, this ratio changes at every iteration
starting from Fk-1 Fk
for the first iteration and reducing k by 1 at every succeeding iteration until
we reach F0 Fk
for the first iteration and reducing k by 1 at every succeeding iteration until
we reach F0 F1
which would be that last iteration (For example F10 F1
which would be that last iteration (For example F10 F11,
F9 F11,
F9 F10,
F8 F10,
F8 F9,
... , F1 F9,
... , F1 F2,
and F0 F2,
and F0 F1). F1).
Example: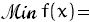 (
(

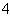 )
2 )
2

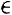 [2 ,5],
[2 ,5],
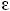 = 0.001 = 0.001
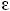 = 0.01 = 0.01
| Step 1: |
k=11,
 = 2,
= 2,  = 5, F10
= 5, F10 F11 =
89/144=0.6180,
1 F11 =
89/144=0.6180,
1 0.6180 = 0.3820, 0.6180 = 0.3820,
 = (5 = (5
 2)(0.3820)
2)(0.3820) 2
= 3.1460, 2
= 3.1460,
 =(5 =(5
 2)(0.6180)
2)(0.6180) 2
= 3.8540, 2
= 3.8540,
 = 0.7293,
= 0.7293,
 = 0.0213
= 0.0213 |
| Step 2: |
 =0.7293 =0.7293
 0.0213=
0.0213= ,
drop interval [2, 3.146). Set: ,
drop interval [2, 3.146). Set:
 =3.1460 =3.1460
 =3.8540 =3.8540
 =0.0213 =0.0213
k=11-1=10
Fk-1 Fk
= F9 Fk
= F9 F10=55/89=0.6179 F10=55/89=0.6179
 = (5 = (5
 3.1460)(0.6179) 3.1460)(0.6179) 3.1460=4.2917 3.1460=4.2917
 =0.0850
and repeat Step 2 =0.0850
and repeat Step 2
|
| Step 2: |
 =0.0213 =0.0213
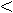 0.0850=
0.0850= ,
drop interval (4.2917, 5]. Set: ,
drop interval (4.2917, 5]. Set:
 =4.2917 =4.2917
 =3.8540 =3.8540
 =0.0213 =0.0213
k=10-1=9
Fk-1 Fk
= F8 Fk
= F8 F9=34/55=0.6182 F9=34/55=0.6182
 =(4.2917-3.1460)(1-0.6182) =(4.2917-3.1460)(1-0.6182) 3.1460=3.5836 3.1460=3.5836
 =0.1733 and
repeat Step 2. =0.1733 and
repeat Step 2. |
Notice how the solution closely relates to the the Golden Section search.
The reason is simple. The Fibonacci ratio of
In eight iterations the interval of Fk-1 Fk
is very close to Fk
is very close to  for large enough k and at the limit it is equal to
for large enough k and at the limit it is equal to
 .
For further discussion on termination rules, please see the discussion at
the bottom of this page. For an interesting
discussion, facts, links, and historical perspectives on Fibonacci numbers and
Golden Ratio in real world check
this
site. .
For further discussion on termination rules, please see the discussion at
the bottom of this page. For an interesting
discussion, facts, links, and historical perspectives on Fibonacci numbers and
Golden Ratio in real world check
this
site.
[ Swann's Method ]
[ Interval Halving Method ]
[ Golden Section Method ]
[ Fibonacci Method ]
Termination:

[ Swann's Method ]
[ Interval Halving Method ]
[ Golden Section Method ]
[ Fibonacci Method ]
|

![]() )
and a step-size parameter (
)
and a step-size parameter (![]() ).
Generate successive points through a recursive relationship and compare the function values at these
successive points. When there is a change in the direction of decrease (for Min problems) the
interval is found. Depending on whether (
).
Generate successive points through a recursive relationship and compare the function values at these
successive points. When there is a change in the direction of decrease (for Min problems) the
interval is found. Depending on whether (![]() ) is at the right of the actual min or to the right of it, the value of
(
) is at the right of the actual min or to the right of it, the value of
(![]() )
may be positive or negative. the recursive relation is:
)
may be positive or negative. the recursive relation is:![]()
![]()
![]()
![]()
![]()
![]() for
for ![]() = 0, 1, 2, ...
= 0, 1, 2, ...![]() , compare
, compare
![]() ,
,
![]() , and
, and
![]() . If:
. If:![]()
![]()
![]()
![]()
![]() , then sign of
, then sign of
![]() is positive.
If:
is positive.
If:![]()
![]()
![]()
![]()
![]() , then sign of
, then sign of
![]() is negative.
is negative.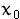
6.5 and step size

0.5. Now let's compare
6.5
7
6
, so
= - 0.5. Now let's generate successive
values and compare their associated f values.
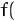
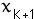
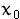
6.5
6.5


+ 1 (-0.5)
6
6


+ 2 (-0.5)
5
5
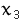

+ 4 (-0.5)
3
3


+8 (-0.5)
-1
-1
![]() over the search are
(
over the search are
(![]() ,
,
![]() ):
):
 (
( (
(
 0.382)
and (
0.382)
and (


![]() over the search are
(
over the search are
(![]() ,
,
![]() ):
):
 0.618,
1
0.618,
1 0.382,
0.382,
 (
(![]() (
(![]()
![]()
![]() )
2
)
2
![]()
![]() [2 ,5],
[2 ,5],
![]() =0.001
=0.001
![]() (
(![]()
![]()
![]() )
2
)
2
![]()
![]() [2 ,5],
[2 ,5],
![]() = 0.001
= 0.001
![]() = 0.01
= 0.01
![]() Fk
is very close to
Fk
is very close to ![]() for large enough k and at the limit it is equal to
for large enough k and at the limit it is equal to
![]() .
For further discussion on termination rules, please see the discussion at
the bottom of this page. For an interesting
discussion, facts, links, and historical perspectives on Fibonacci numbers and
Golden Ratio in real world check
this
site.
.
For further discussion on termination rules, please see the discussion at
the bottom of this page. For an interesting
discussion, facts, links, and historical perspectives on Fibonacci numbers and
Golden Ratio in real world check
this
site.![]()